Number Theory

Divisibility

The Euclidean Algorithm

The Diophantine Equation

Congruences

Let $a,$, $b$ and $n$ be integers. If $n\neq 0$, we say that $a$ is congruent to $b$ modulo $n$ if $a-b$ is divisible by $n$, which is written $a\equiv b(\text{mod}\ n)$.

If $a\equiv b(\text{mod}\ n)$ and $b\equiv c(\text{mod}\ n)$, then $a\equiv c(\text{mod}\ n)$.
If $a\equiv b(\text{mod}\ n)$, then for any $c$, $a\pm c\equiv b\pm c(\text{mod}\ n)$ and $ac\equiv bc(\text{mod}\ n)$.
If $a_1\equiv b_1(\text{mod}\ n)$ and $a_2\equiv b_2(\text{mod}\ n)$, then $a_1\pm a_2\equiv b_1\pm b_2(\text{mod}\ n)$ and $a_1a_2\equiv b_1b_2(\text{mod}\ n)$ .
For any positive integer $c$, the statement $a\equiv b(\text{mod}\ n)$ is equivalent to the congruences $a\equiv b,b+n,\ldots,b+(c-1)n\ (\text{mod}\ n)$.
If $ab\equiv ac(\text{mod}\ n)$, then $b\equiv c(\text{mod}\ n)$ if $\text{gcd}(a,n)=1$ or $b\equiv c(\text{mod}\ \frac{n}{d})$ if $d=\text{gcd}(a,n)>1$.
Fermat’s Little Theorem. If $p$ is a prime and $a$ is an integer, then $a^p\equiv a(\text{mod}\ p)$ for any $a$, and $a^{p-1}\equiv 1(\text{mod}\ p)$ if $p$ does not divide $a$.

Abstract Algebra

Groups

Let $S$ be a nonempty set, then a binary operation on $S$ is a function $f:S\times S\rightarrow S$ (closed under the binary operation). $f(a,b)$ is usually denoted by $a\ast b$ for $a,b\in S$. A nonempty set $S$, together with a binary operation defined on it, is called a binary structure.

A binary structure whose binary operation is associative, i.e., $(a\ast b)\ast c=a\ast (b\ast c)$ is called a semigroup.

The element $e$ of $S$ with the property that $a\ast e=e\ast a=a,$ for every $a\in S$ is called the identity. The identity may not exist for some binary structures. A semigroup that has an identity is called a monoid.

Let $(S,\ast )$ be a monoid, if $\forall\ a\in S$, $\exists\ a^{-1}\in S$ being the inverse of $a$, such that $aa^{-1}=a^{-1}a=e,$ then $(S,\ast )$ is a group.

Examples:

$(\mathbb{Z},+),e=0$.
$GL_n(\mathbb{R})$, invertible real $n\times n$ matrices with matrix multiplication, $e=I$.
$(\mathbb{Q}\setminus\{0\},\cdot),e=1$.
Symmetric group $S_n$, bijections from $\{1,2,\ldots,n\}$ to $\{1,2,\ldots,n\}$ with composition as the group operation. $S_n$ can be viewed as permutation of the set $\{1,2,\ldots,n\}$.

A semigroup, monoid, or group whose binary operation is commutative, i.e. $a\ast b=b\ast a,$ is said Abelian.

Common notations. We usually just write $ab$, instead of $a \ast b$, even if the operation isn’t ordinary multiplication. Also, if the binary operation is commutative, it’s common to see it denoted by $+$, even if the operation isn’t ordinary addition.

Examples:

$(\mathbb{Z},+),e=0$.
$(\mathbb{Q}\setminus\{0\},\cdot),e=1$.
$(\mathbb{R}^{n\times n},+),e=\mathbf{0}$.
$\mathbb{Z}[x],\mathbb{Q}[x],\mathbb{R}[x],$ polynomial group with addition.

A group $G$ with the property that there’s an element $a$ in $G$ such that $G=\{a^n:n=0,1,2,\ldots\}$
is said to be cyclic, and the element $a$ is a generator of the group.

The integer $m$ is a generator of $(\mathbb{Z}_n,\oplus)$ if and only if $m$ is relatively prime to $n$.
Let $G$ be a cyclic group with generator $a$. The element $a^m$ is a generator of $G$ if and only if $m$ is relatively prime to $n$.

If a pair of groups are isomorphic, then all their structural properties are identical.

Subgroup

Let $(G, \ast )$ be a group. If there’s a subset $H$ of $G$ such that $(H, \ast )$ is also a group, then we say that $H$ is a subgroup of $G$, and write $H \leq G$. If $H\neq G$, then $H$ is a proper subgroup of $G$, denoted by $H<G$. The trivial subgroups of $G$ are $\{e\}$ and $G$.

The cyclic subgroup generated by $a\in G$ is given by $\langle a\rangle=\{a^n:n\in\mathbb{Z}\}$. The order of an element of a group is the order of $\langle a\rangle$.

Examples:

The conjugation $gHg^{-1}=\{gxg^{-1},x\in H\}$ for $H\leq G$ and $g\in G$ is a subgroup of $G$.

If $\forall\ g\in G,gHg^{-1}=H$, then $H$ is a normal subgroup of $G$, denoted by $H\lhd G$ $(\{e\}\lhd G,G\lhd G)$. Any subgroup of abelian group is normal.

Given a group $H\lhd G$, define an equivalence relation $x\sim y\ \Leftrightarrow\ xy^{-1}\in H$, then the set of equivalent classes $G/H$ is a group, called a quotient group (not a subgroup of $G$).

Examples:

$k\mathbb{Z}\lhd\mathbb{Z}$, $a\sim b\ \Leftrightarrow\ a+(-b)\in k\mathbb{Z}$, $\mathbb{Z}/k\mathbb{Z}=\mathbb{Z}_k=\langle \overline{1}\rangle$.

The order of a group is $|G|$, the number of elements in a group. The index of a subgroup is $[G:H]=\frac{|G|}{|H|}$. If the subgroup is normal, then $[G:H]=|G/H|$. The order of an element $g\in G$ is $|\langle g\rangle|$, which is the minimal positive integer $n$ for which $g^n=e$.

Properties:

If $H\leq G$, then $|H|$ divides $|G|$.
For any $g\in G$, $g^{|G|}=e$.
Any subgroup of index 2 is normal.

For some groups, particularly large ones, it’s often more economical to specify a set of generators and a set of equations connecting them-called relations-that can be used to reconstruct the entire group table. Together, the set of generators and set of relations is called a presentation of the group.

Lagrange’s Theorem. Let $G$ be a finite group. If $H$ is a subgroup of $G$, then the order of $H$ divides the order of $G$.
Let $G$ be a finite, Abelian group of order $n$. Then $G$ has at least one subgroup of order $d$ for every (positive) divisor $d$ of $n$.
Let $G$ be a finite, cyclic group of order $n$. Then $G$ has exactly one subgroup-a cyclic subgroup-of order $d$ for every (positive) divisor $d$ of $n$, i.e., $G=\langle a\rangle$ if and only if $gcd(a,|G|)=1$. If $G$ is generated by $a$, then the subgroup generated by the element $b=a^m$ has order $d = \frac{n}{\text{gcd}(m, n )}$. [If $m = 0$, then we’ll agree that $\text{gcd}(m, n) = n$.]
Cauchy’s Theorem. Let $G$ be a finite group of order $n$, and let $p$ be a prime that divides $n$. Then $G$ has at least one subgroup of order $p$.
Sylow’s First Theorem. Let $G$ be a finite group of order $n=p^km$, where $p$ is a prime that does not divide $m$.Then $G$ has at least one subgroup of order $p^i$ for every integer $i$ from $0$ to $k$.

Group Homomorphisms

Let $(G,\cdot)$ and $(G’,\ast )$ be groups. A function $\phi:G\rightarrow G’$ with the property that $\phi(a\cdot b)=\phi(a)\ast \phi(b)$
for all elements $a$ and $b$ in $G$, is called a group homomorphism.

If $e$ is the identity in $G$, then $\phi(e)$ is the identity in $G’$.
If $g\in G$ has finite order $m$, then $\phi(g)\in G’$ also has order $m$.
If $a^{-1}$ is the inverse of $a$ in $G$, then $\phi(a^{-1 })$ is the inverse of $\phi(a)$ in $G’$.
If $H$ is a subgroup of $G$, then $\phi(H)$ is a subgroup of $G’$, where $\phi(H)=\{\phi(h):h\in H\}$.
If $G$ is finite, then the order of $\phi(G)$ divides the order of $G$; if $G’$ is finite, then the order of $\phi(G)$ also divides the order of $G’$.
If $H’$ is a subgroup of $G’$, then $\phi^{-1} (H’)$ is a subgroup of $G$, where $\phi^{-1}(H’)=\{h\in G:\phi(h)\in H’\}$.

A homomorphism that’s one-to-one (injective) is called a monomorphism; if it’s onto (surjective), it’s called an epimorphism; and if it’s one-to-one and onto (bijective), it’s called an isomorphism. A homomorphism from a group to itself is called an endomorphism, and an isomorphism from a group to itself is called an automorphism.

A homomorphism is a monomorphism if and only if its kernel $\text{ker}\phi=\{g\in G:\phi(g)=e’\}$ is trivial.
The kernel of a group homomorphism $\phi: G\rightarrow G’$ is always a subgroup of $G$.

Direct Product And Direct Sum

The direct product of the groups $(G_1,\ast_1)$ and $(G_2,\ast_2)$ is the group $(G_1\times G_2,\ast)$ where $G_1\times G_2=\{(a,b):a\in G_1,b\in G_2\}$ and $*$ is the defined binary operation such that $(a_1,a_2)\ast(b_1,b_2)=(a_1\ast_1 b_1,a_2\ast_2 b_2).$

For Abelian groups, we use the notation $G_1\oplus G_2$ and call it as direct sum.

The direct sum $\mathbb{Z}_m\oplus \mathbb{Z}_n$ is cyclic if and only if $\text{gcd}(m, n) = 1$. If this is the case, then, $\mathbb{Z}_m\oplus \mathbb{Z}_n$ is isomorphic to $\mathbb{Z}_{mn}$.
The direct sum $\mathbb{Z}_{m_1}\oplus \cdots \oplus\mathbb{Z}_{m_k}$ is cyclic if and only if $\text{gcd}(m_i , m_j) = 1$ for every distinct pair $m_i$ and $m_j$. If this is the case, then $\mathbb{Z}_{m_1}\oplus \cdots \oplus\mathbb{Z}_{m_k}$ is isomorphic to $\mathbb{Z}_{m_1m_2\cdots m_k}.$
Every finite Abelian group $G$ is isomorphic to a direct sum of the form $\mathbb{Z}_{p_1^{k_1}}\oplus\cdots\oplus \mathbb{Z}_{p_r^{k_r}}$ where the $p_i$ are (not necessarily distinct) primes and $k$ are (not necessarily distinct) positive integers. The collection of prime powers $p_i^{k_i}$ for a given representation of $G$, are known as the elementary divisors of $G$.
Every finite Abelian group G is isomorphic to a direct sum of the form $\mathbb{Z}_{m_1}\oplus\cdots\oplus \mathbb{Z}_{m_t}$ where $m_1\geq 2$, $m_{i-1}$ divides $m_{i}$ for $i=1,\ldots,t.$ The distinct list $m_1,\cdots,m_t$ is called the invariant factors of $G$.

Rings

A set $R$, together with two binary operations (we’ll use addition, $+$, and multiplication, $\cdot$), is called a ring if the following conditions are satisfied:

$(R,+)$ is a Abelian group;
$(R,\cdot)$ is a semigroup;
the distributive laws hold; that is, for every $a$, $b$, and $c$ in $R$, we have: $a*(b+c)=a\ast b+a\ast c\qquad (a+d)\ast c=a\ast c+d\ast c.$

The smallest positive integer $n$ such that $na = 0$ for every $a$ in R (if such an $n$ exists) is called the characteristic of the ring, and we write $\text{char} R = n$.

If the multiplicative semigroup $(R, \cdot )$ is a monoid-that is, if there’s a multiplicative identity-then $R$ is called a ring with unity. The identity of the additive abelian group $(R, +)$ is usually denoted by $0$ and, in a ring with unity, the identity of the multiplicative monoid $(R, \cdot )$ is usually denoted by 1.

If the operation of multiplication is commutative, then we call $R$ a commutative ring. (The term abelian is generally not used to describe a ring in which multiplication is commutative.)

If $S$ is a subset of $R$, and $S$ satisfies the ring requirements with the same operations as $R$, then we say that $(S, +, \cdot )$ is a subring of $(R, +, \cdot)$.

ring of polynomial. The ring of polynomials with coefficients in a ring $R$ is usually denoted by $R[x_1,\cdots,x_n]$ or $R[x]$ where $x$ refer to the set of variables $\{x_1,\cdots,x_n\}$. An element $f(x)\in \mathbb{R}[x]$ can be written as a finite sum $f(x)=\sum\limits_b b_{\alpha} x^{\alpha},$
where $\alpha=(\alpha_1,\cdots,\alpha_d)$ is a multi-index and $\alpha_i\in \mathbb{R}$.

Let $I$ be a subring of a ring $R$. If $\forall\ r\in R,x\in I$, $rx\in I$ and $xr\in I$, then $I$ is called an ideal on $R$. Every ring $R$ has at least two ideals, $\{ 0 \}$ and $R$.

Ring Homomorphisms

Let $(R, +, \times)$ and $(R’, \oplus,\otimes)$ be rings. A function $\phi: R \rightarrow R’$ is called a ring homomorphism if both of the following conditions hold for be every $a$ and $b$ in $R$:

$\phi(a+b)=\phi(a)\oplus\phi(b).$
$\phi(a\times b)=\phi(a)\otimes\phi(b).$

The kernel of a ring homomorphism is the set $\text{ker}\phi=\{a \in R : \phi(a) = 0’\}$, where $0’ $ is the additive identity in $R’$ and is always a subring of $R$.
The image of $R$, $\phi(R)=\{\phi(r):r\in R\}$ is a subring of $R’$.
The image of $0$, the additive identity in $R$, must be $0’$.

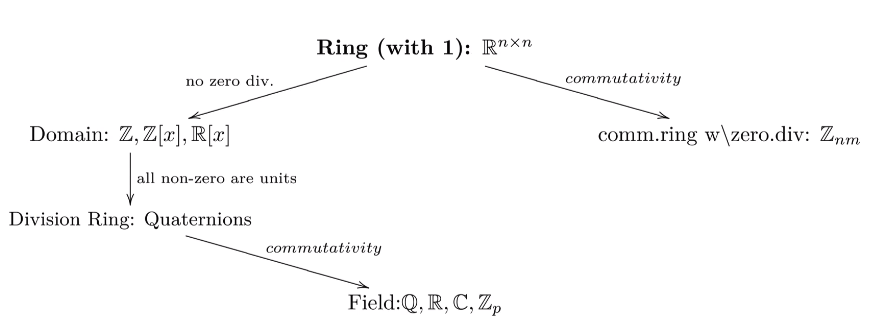
Domains

A domain is a nonzero ring with unity, in which $ab = 0$ implies $a = 0$ or $b = 0$.

A commutative domain is called an integral domain.

The cancellation law holds for domains.

Fields

Let $a$ be a nonzero element of a ring $R$ with unity. If $a$ is invertible, then $a$ is called a unit. If every nonzero element in $R$ is a unit, i.e. $(R^{\ast },\cdot)$ is a group, then $R$ is called a divison ring. A division ring is a ring with exactly two ideals.

A commutative division ring is called a field. A domain where all non-zero elements are units is a field.

Every finite integral domain is a field. A finite division ring must be commutative.

The ring $\mathbb{Z}_n$ is a field if and only if $n$ is a prime.

The field has no zero divisors since a zero divisor is not invertible.