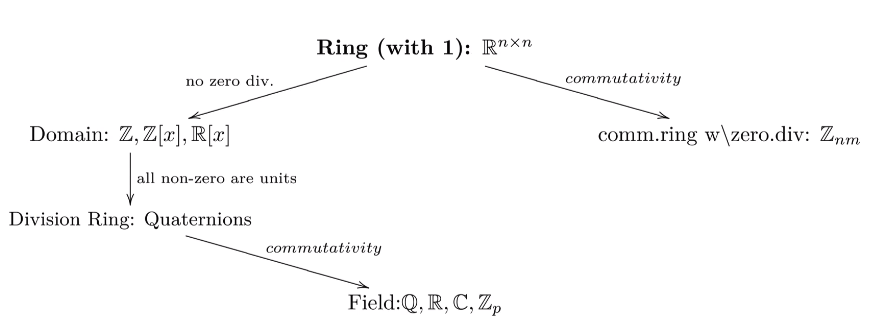
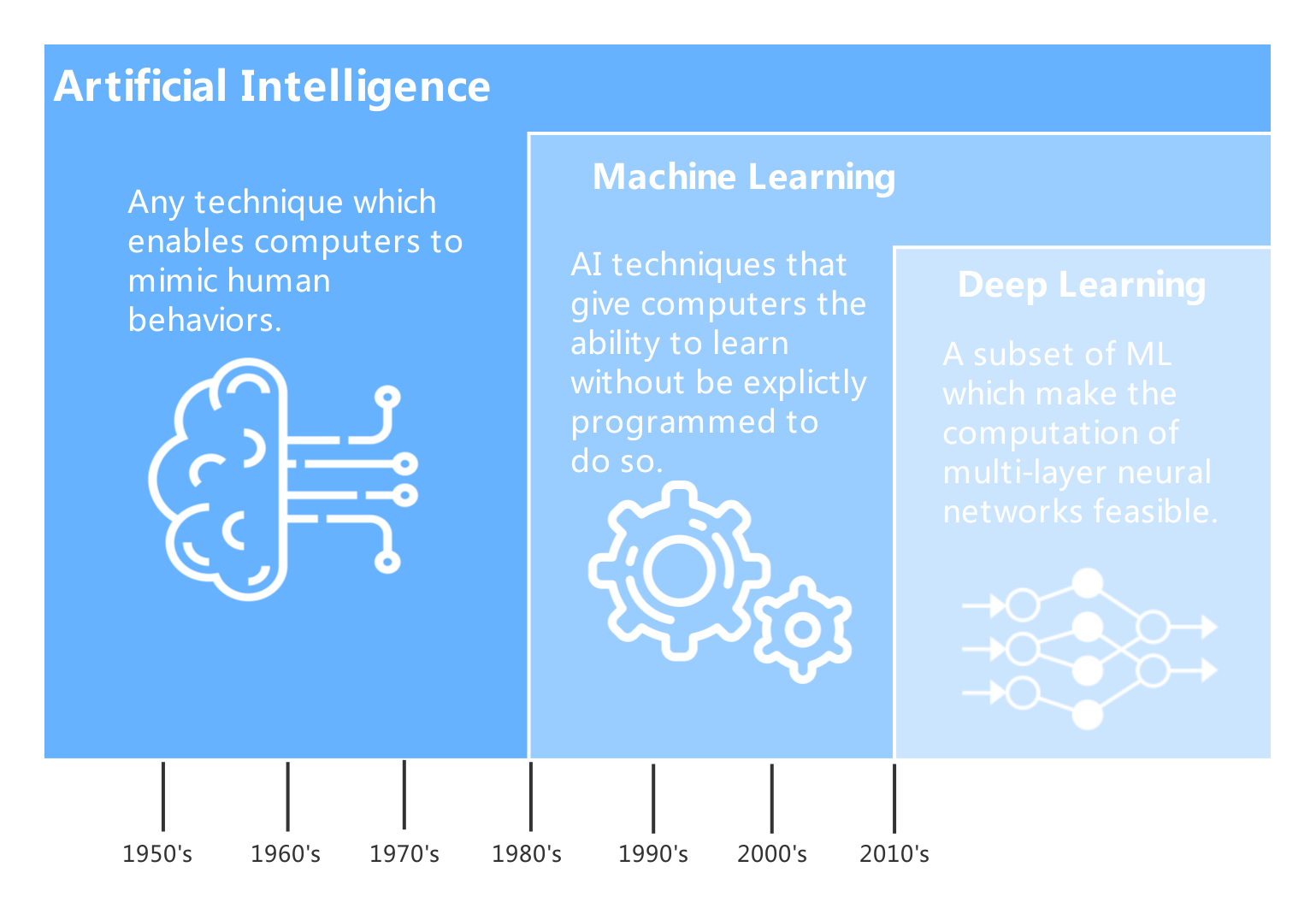
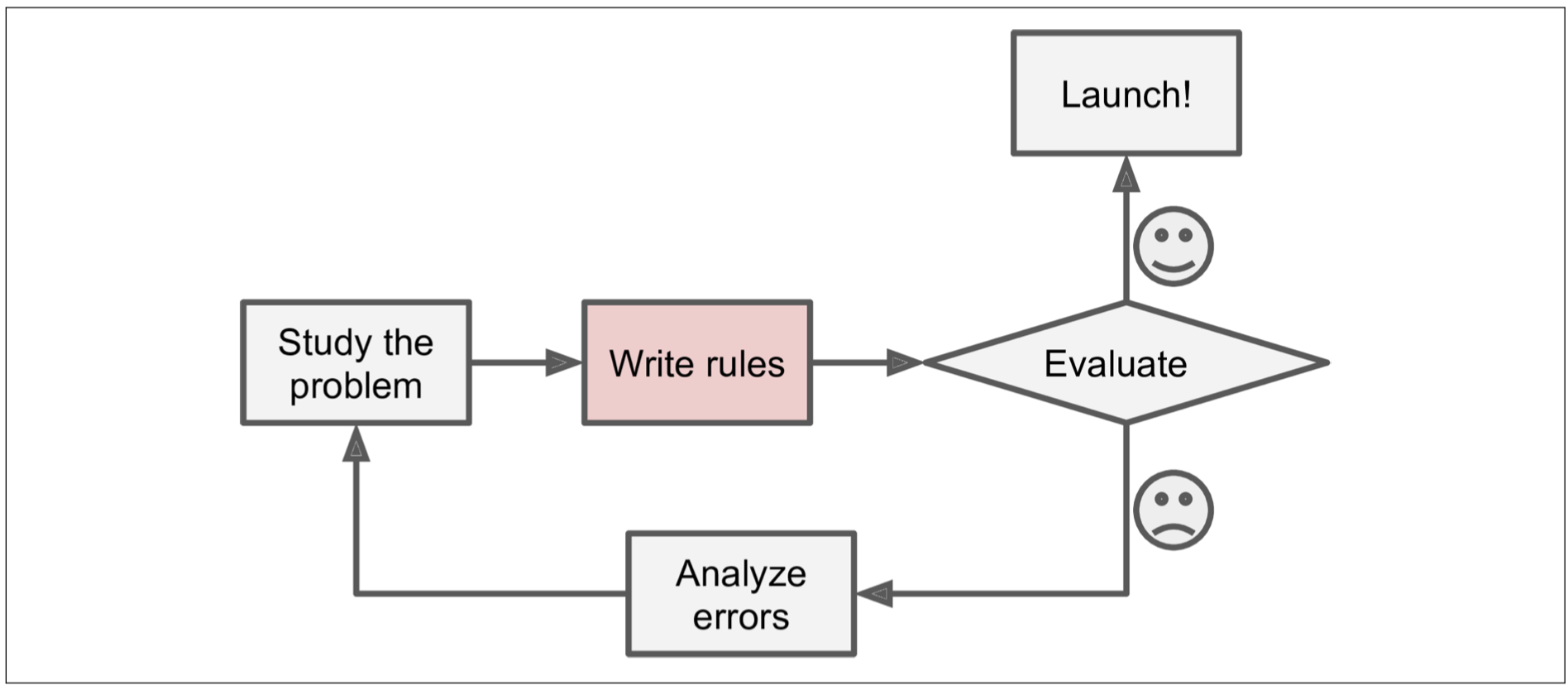
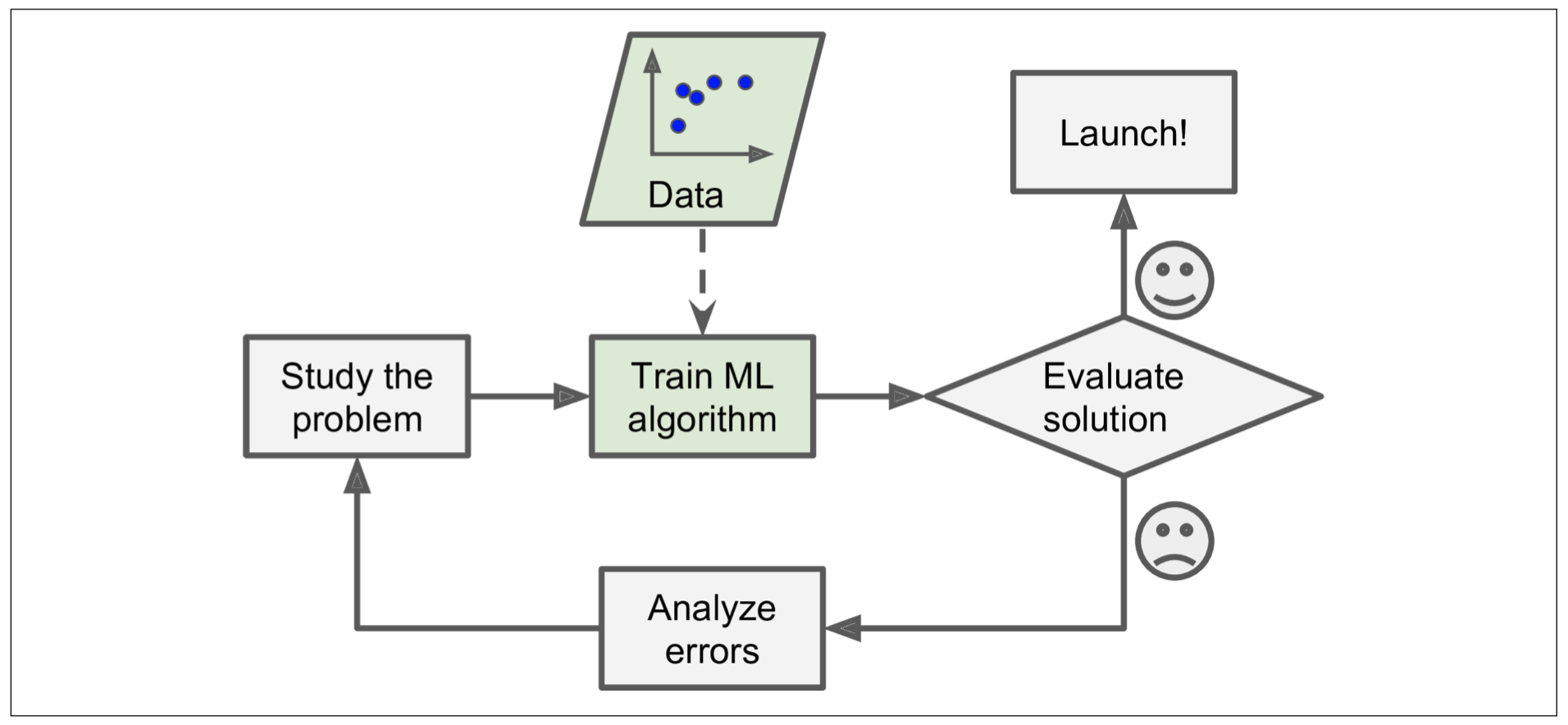
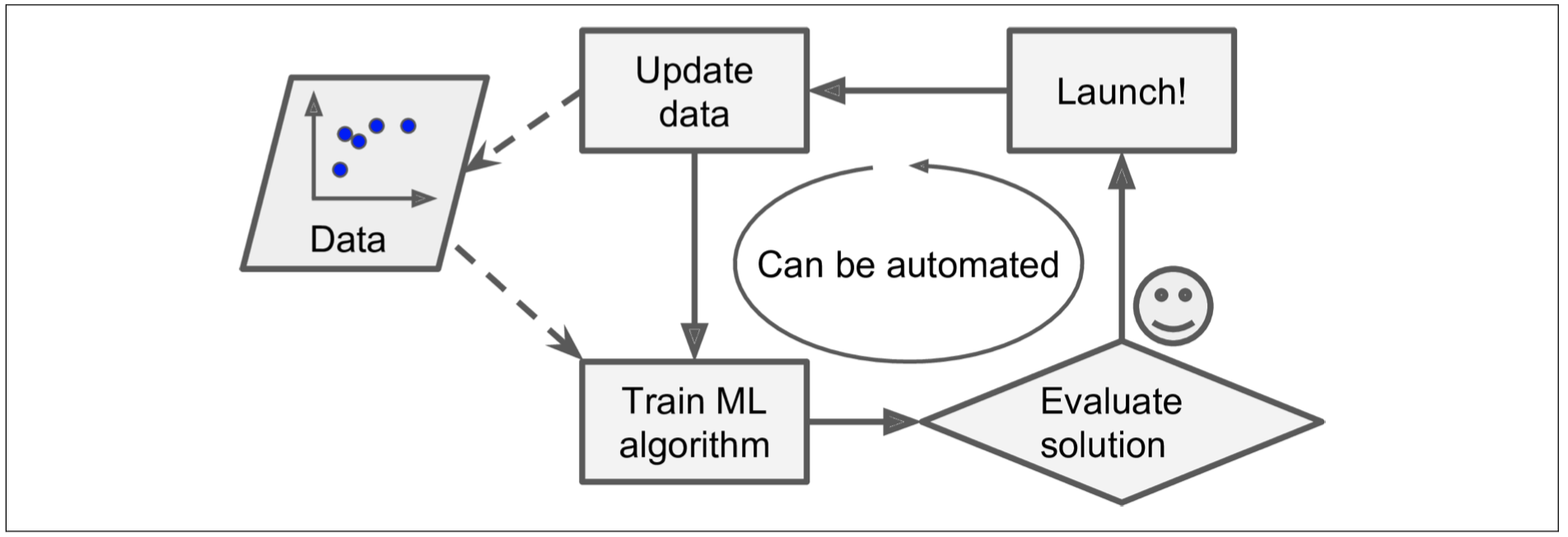
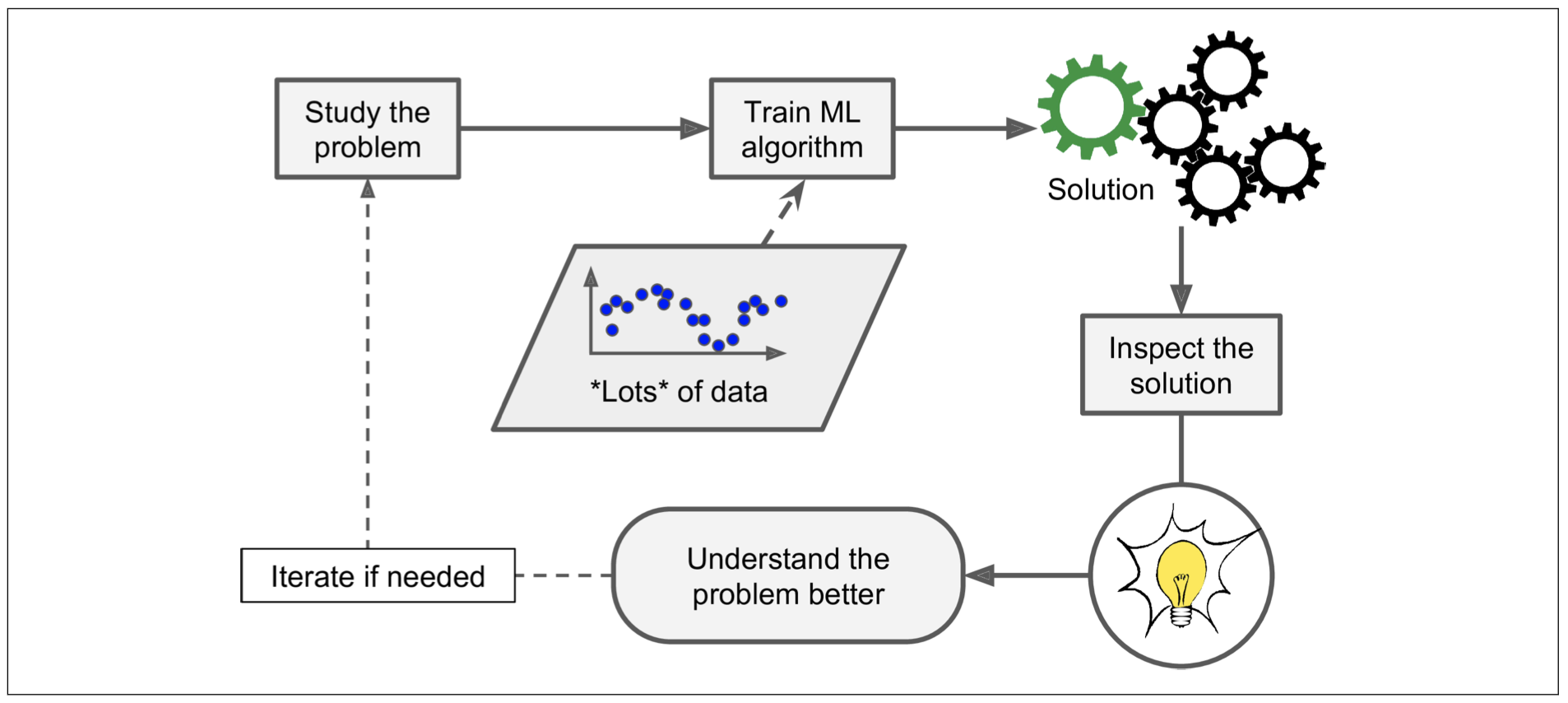
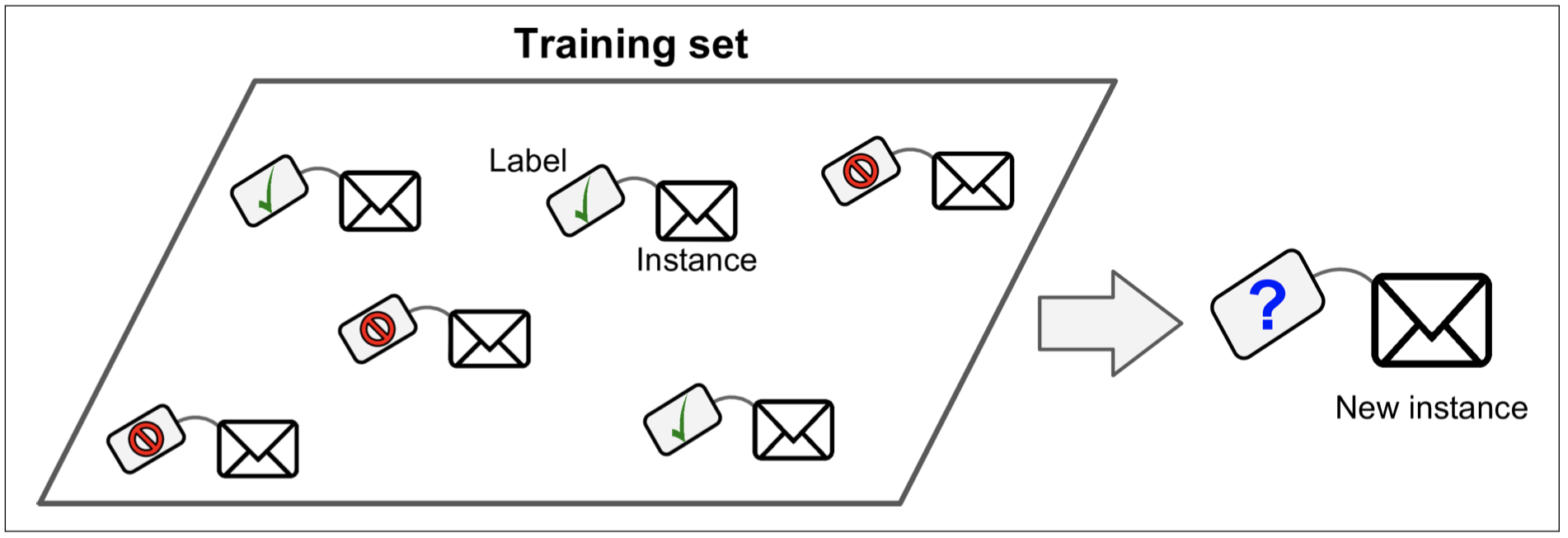
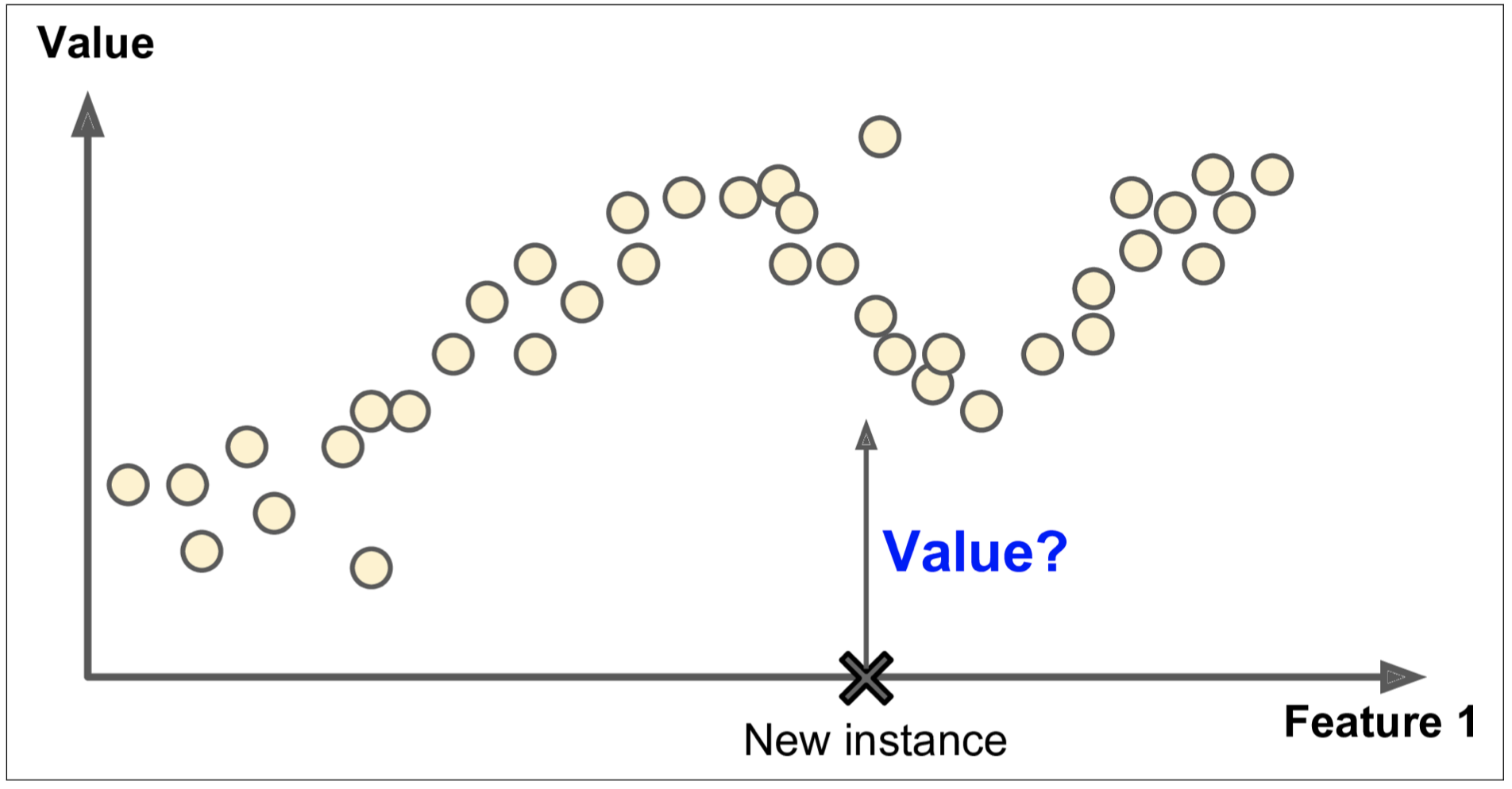
Statistics
| Course Name | Github | BaiduDisk |
|---|---|---|
| STAT 30100 - Mathematical Statistics | link | |
| STAT 30400 - Distribution Theory | link | de7j |
| STAT 30900 - Mathematical Computation I:Matrix Computation | link | cq9v |
| STAT 34300 - Applied Linear Statistical Model | link | y79v |
| STAT 34700 - Generalized Linear Models | link | |
| STAT 34800 - Modern Methods in Applied Statistics | link |
Computer Science
| Course Name | Github | BaiduDisk |
|---|---|---|
| TTIC 31250 - Introduction to Theory of Machine Learning | link |