This post summarizes multiple testing.

The multiple testing problem is behind a lot of the "reproducibility crisis" of modern science. Many results that have been reported significant cannot be reproduced simply because they are false rejections. Most of such false discoveries come from doing multiple testing but not properly adjusting the tests to reflect the fact that many hypothesis tests are being done. The basic question of doing multiple testing is how to adjust our $p$-value cutoffs to account for the fact that multiple tests are being done.

Family-Wise Error Rate

Suppose that we are testing $d$ null hypotheses $H_{1},\ldots,H_d$ and denote the set of null and alternative hypotheses by $\mathcal{H}_0$ and $\mathcal{H}_1$ respectively. The Family-Wise Error Rate (FWER) is the probability that we falsely reject any null hypothesis: $$FWER=\mathbb{P}({\exists\ i\in\mathcal{H}_0, \text{ such that } H_{i} \text{ is rejected}}).$$

Sidak Correction

The Sidak correction procedure rejects the $i$th test if: $$p_i\leq 1- (1-\alpha)^{1/d}.$$

If the $p$-values are all independent, then with Sidak correction, $FWER \leq\alpha$.

Bonferroni Correction

The Bonferroni correction procedure rejects the $i$th test if: $$p_i\leq \frac{\alpha}{d}.$$

With Bonferroni correction, $FWER \leq\alpha$. Compared to Sidak correction, we do not need the independence of all $p$-values.

Holm's Procedure

There are many improvementto the Bonferroni procedure. For example, if we know eactaly that there are $d_0$ null hypotheses, we can use cutoff $\frac{\alpha}{d_0}$. Similar idea yields the Holm's procedure, where the cutoff is determined adaptively.

1. Order the $p$-values $p_{(1)}\leq\cdots\leq p_{(d)}$.
2. If $p_{(1)}\leq \frac{\alpha}{d}$, then reject $H_{(1)}$ and move on; else stop and aceept $H_{(1)},\ldots,H_{(d)}$.
3. If $p_{(2)}\leq \frac{\alpha}{d-1}$, then reject $H_{(2)}$ and move on; else stop and aceept $H_{(2)},\ldots,H_{(d)}$.
4. $\vdots$
5. If $p_{(d)}\leq \alpha$, then reject $H_{(d)}$; else stop and aceept $H_{(d)}$.

Equivalently, we reject $H_{(i)}$ for $i\leq i^*=\min\{i:p_{(i)}\geq \frac{\alpha}{d-i+1}\}$.

Holm's procedure also controls the FWER at level $\alpha$.

False Discovery Rate

The false discovery rate (FDR) is the expected number of false rejections divided by the number of rejections. Given hypotheses $H_1,\ldots,H_d$, denote the number of false rejections as $V$, and the total number of rejections as $R$. Then the false discovery proportion is: $$FDP=\begin{cases}\frac{V}{R}&,\text{ if }R>0\\0&,\text{ if }R=0.\end{cases}$$ Then FDR is given by $$FDR=\mathbb{E}[FDP].$$ We can see that $$FWER=\mathbb{P}(V\geq 1)\geq \mathbb{E}\left[\frac{V}{R}\mid R>0\right]\mathbb{P}(R>0)=FDR,$$ since $\frac{V}{R}\leq 1$. Thus FWER control implies FDR control, and FDR control is less stringent and may give more power.

BH Procedure

The Benjamini-Hochberg (BH) procedure is given by

1. Order the $p$-values $p_{(1)}\leq\cdots\leq p_{(d)}$.
2. Find the largest $i_{\max}$ such that $i^*=\mathop{\arg\max}\{i:p_{(i)}\leq \frac{i\alpha}{d}\}$.
3. Reject $H_{(1)},\ldots,H_{(i^*)}$ .

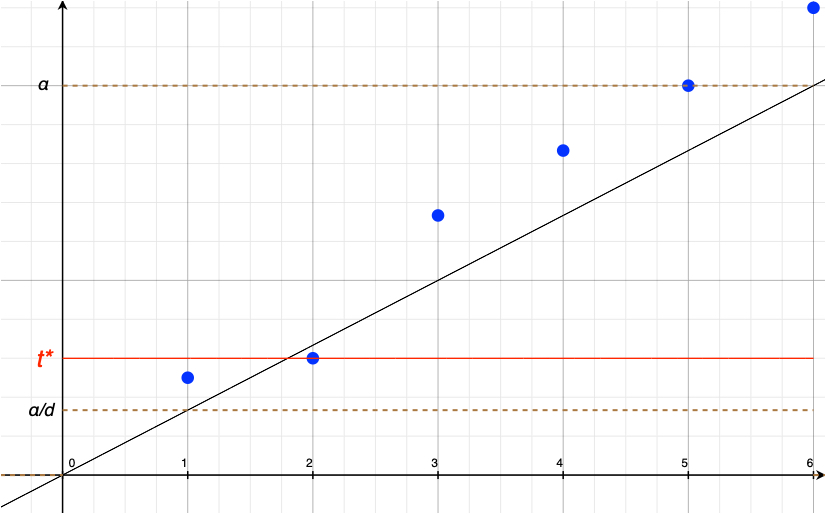
It is equivalent to reject any hypothesis with $p_i\leq t^{\ast}=\frac{i^{\ast}\alpha}{d}$.

If the $p$-values are all independent, then with BH procedure, $FDR \leq\alpha$.